これまでの発表論文全体については、
などをご覧ください。以下には、これまでの研究成果(論文)の一部と、研究の経緯などを紹介します。 自分で気に入っているという判断基準ですが、気まぐれも含むので、必ずしもここに取り上げたものが取り上げていないものよりも重要であるとは限りません。 また、研究の発端から書いていくと、昔の話が多めになってしまいました。 まだまだ紹介したい研究はたくさんあるので、最近の研究を含め、内容はおいおい追加していきたいと思います。
記念すべき(?)初めての論文なので思い入れがあるのですが、それだけではなくて、その後の多くの研究のきっかけになりました。 主な内容としては、Kennedy-TasakiがS=1量子スピン鎖について発見した「隠れたZ2×Z2対称性」を引き出す変換の簡潔な表示を 見つけ、これを用いて一般の整数スピン鎖に拡張したというものです。 大学院入学当初、量子スピン系もHaldane予想も何も知らなかったのですが、たまたまM1のときに参加した「物性若手夏の学校」で 田崎晴明さんの講義 (その講義録←入門記事としてお勧め!) に出席して、興味を持ちました。 その後、学習院の田崎さんの研究室にお邪魔して、Kennedy-Tasaki論文のプレプリント(印刷したもの:当時はまだarXivが無かった!) をお借りして、それを見ていろいろ式をいじっていたら、Kennedy-Tasaki変換のうまい表式が見つかりました (翌年の夏、京都の国際会議をモグ…で聴講中、泊まっていた宿で計算していてできた記憶が。)
このとき、計算してみると、整数スピンの中でも奇数スピンを持つスピン鎖では隠れた対称性が自発的に破れており、偶数スピンだと破れていない、 結果となったのですが、その意味は長い間よくわかりませんでした。 その後20年近く経った2009年になって、前者は非自明なSymmetry-Protected Topological相 (対称性によって守られたトポロジカル相、SPT相)であることがわかりました。 この1992年の論文の時点でよくよく考えていたらSPT相の概念に到達できたはずなのですが… 出版当時はマイナーな論文でしたが、SPT相の発見にともない、よく引用してもらえるようになりました。 SPT相関連については、また改めて書こうと思います。
上で触れた「隠れた対称性の一般化」論文の中で、部分的に磁化したAKLT状態を構成して、その状態における隠れた対称性の破れを
論じました。
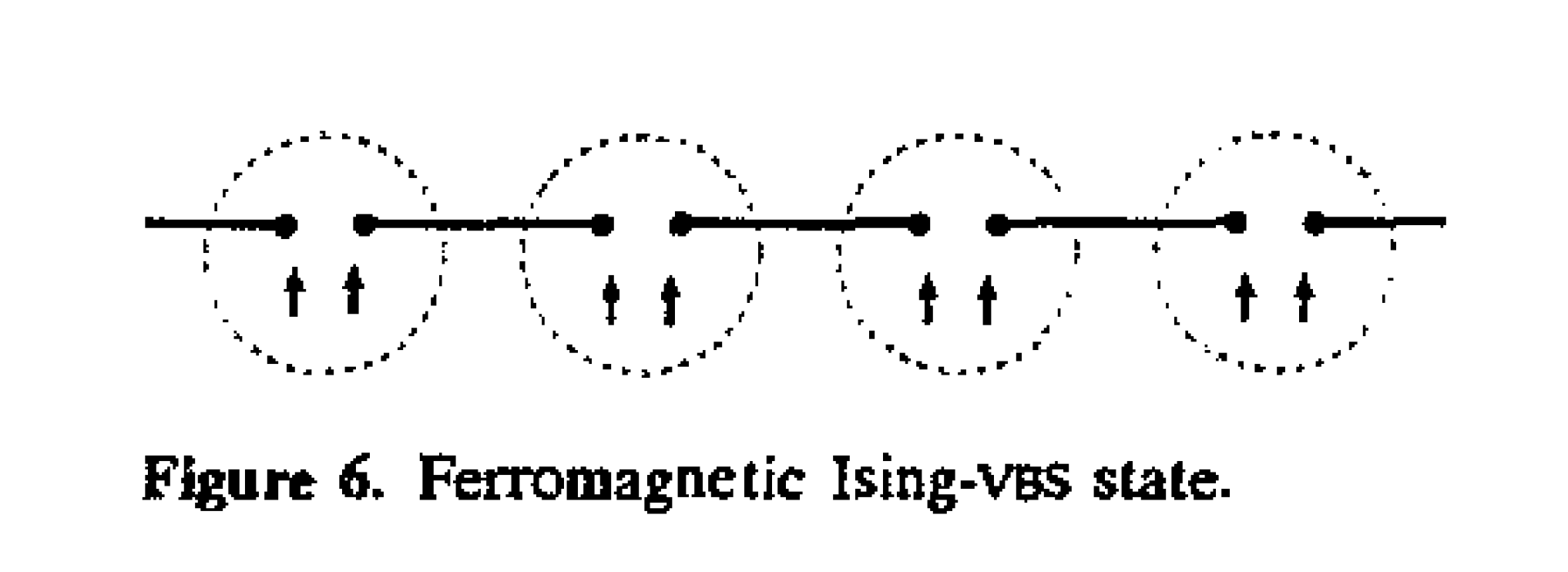
1995年秋から、Ian Affleckのポスドクとしてカナダ・バンクーバーのUniversity of British Columbia (UBC)に行きました。 ↑の、部分的に磁化したAKLT状態の話を相談すると、それはLieb-Schultz-Mattis (LSM)定理に関係するんじゃないか、 とすぐに示唆してくれました。 そこから、U(1)対称性を持つ量子スピン鎖で励起ギャップを持つ「磁化プラトー」が出現するための量子化条件がすぐに導かれました↓
Masaki Oshikawa, Masanori Yamanaka, and Ian Affleck, Magnetization Plateaus in Spin Chains: “Haldane Gap” for Half-Integer Spins Phys. Rev. Lett. 78, 1984 (1997) ,その後、LSM定理は(技術的には何の困難もなく)電子系にも適用でき 固体電子論の基本であるLuttinger定理の非摂動論的な「証明」を与えることもわかりました↓
Masanori Yamanaka, Masaki Oshikawa, and Ian Affleck, Nonperturbative Approach to Luttinger's Theorem in One Dimension, Phys. Rev. Lett. 79, 1110 (1997) ,電子系にも適用してみると、LSM定理の本質は粒子密度と格子の「整合性」にあることがはっきりします。 ミステリアスだったHaldane予想(整数スピン鎖と半奇数スピン鎖の差異)も、 量子スピン鎖を多粒子系と解釈すれば整合性条件の帰結に他なりません。 直観的には、整合性条件は次元によらず重要なはずです。 そこで、LSM定理を高次元に拡張することを考えました。 LSMの原論文の最後の方に、サイズが異方的な極限(縦と横を同時に無限大にするが、縦横比がゼロに近づくようにする) ではLSMの1次元的な証明が高次元系に適用できることはコメントされているのですが、そういうめっちゃ細長い系を 高次元系とみなして良いのかはよくわかりませんでした。 (今から振り返ってみると、本質的にはそれでも良かった気もします。まあ、これは、 サイズが等方的な高次元系でちゃんと示されたので、そうも思えるのでしょう。)
しばらく糸口がつかめなかったのですが、Laughlinが量子ホール効果でホール伝導度が量子化されることを示す 議論に用いた、Aharonov-Bohm磁束の断熱挿入を考えればよい、とふと思いつきました。 (UBCにいた頃から考えていましたが、これを思いついたのは東工大に移ってからです。) それで書いたのが↓です。
Masaki Oshikawa, Commensurability, Excitation Gap, and Topology in Quantum Many-Particle Systems on a Periodic Lattice , Phys. Rev. Lett. 84, 1535 (2000),この話はAharonov-Bohm磁束の挿入でギャップが閉じない(物理的にはリーズナブルだが非自明な)仮定に依存しているので ちゃんとした証明ではありませんが、その後Hastingsらによって厳密な証明が与えられています。 (Lieb-Schultz-Mattis-Oshikawa-Hastings theoremと呼ばれることもあります。) 一方、ここで使ったflux insertion argumentはいろいろと応用ができて、この後何度も役に立ちます。 まず、 "flux insertion argument"でやはり一般次元のLuttingerの定理の非摂動的な「証明」もできる、 というのが↓の論文です。
Masaki Oshikawa, Topological Approach to Luttinger's Theorem and the Fermi Surface of a Kondo Lattice, Phys. Rev. Lett. 84, 3370 (2000) ,この話は、Subir Sachdev氏の講義や、 同氏による最近の教科書Quantum Phases of Matterでもかなり丁寧に解説して頂いています。
一般化されたLSM定理、あるいは整合性条件による制約、は2010年代以降ふたたび盛んに研究され、さまざまに拡張されています。 LSM原論文の議論の現代的な解説は田崎さんの教科書 Physics and Mathematics of Quantum Many-Body Systems (Graduate Texts in Physics)が、 最近のさまざまな拡張に関する解説は、渡辺悠樹君による 量子多体系の対称性とトポロジー: 統一的な理解を目指して (SGCライブラリ 179)が良いと思います。 僕自身も関連する研究を最近もやっているので、また追記するかもしれません。
(前史) 上述のように、LSM定理の「証明」ではAB磁束の印加によってギャップが閉じないことを仮定していました。 この仮定を外したいと思っていろいろ考えたのですが、ギャップの有無を直接論じるのを止めて、系のDrude重みに着目することを思いつきました。 AB磁束の断熱的な印加によってエネルギーが増えてしまうなら、(次元にもよりますが)Drude重みが正の完全導体になっていることがわかります。 これを整合性条件と結びつけることができました。
Masaki Oshikawa, Insulator, Conductor, and Commensurability: A Topological Approach Phys. Rev. Lett. 90, 236401 (2003) ; Erratum Phys. Rev. Lett. 91, 109901 (2003) ,その後だいぶ経って、LSMの原論文で用いられた変分励起状態は、AB磁束を瞬間的に印加するクエンチ操作の後の状態と解釈できることに 気づき、クエンチ後の状態と初期状態(基底状態)の内積で定義される「分極振幅」に興味を持つようになりました。 (電気分極と分極振幅については別項目で書くことにします。) 分極振幅について考えていて煮詰まったのですが、ふと、内積のかわりに、クエンチ後の状態でのハミルトニアンの期待値を考えてはどうかと 思いました。これは、AB磁束の瞬間的な印加に伴うエネルギー増加を与えますが、エネルギー増加と電流の関係を用いると、 これは線形応答の範囲では範囲では、光学伝導度の 全周波数積分に関係づけられます。これによって、線形の光学伝導度について知られている「周波数和則」を導くことができます。 さらに、これは線形にとどまらず、任意の次数の非線形伝導度についての周波数和則を自然に導きます。 (このあたりは、Harvard CMSAに滞在していた際、地下のオフィスで唸っているうちにできたような気がします。) 最初、一人で論文を書いたのですが、渡辺悠樹君がいろいろ拡張してくれて、さらに、AB磁束の断熱印加を考えれば Drude重みのKohn公式の非線形版を導ける、ことを指摘してくれました。 (2003年にDrude重みの論文を書いているので、最初から僕が気づいていても良さそうなものでしたが…) それでできた論文が↓です。
Haruki Watanabe and Masaki Oshikawa, Generalized f-sum rules and Kohn formulas on nonlinear conductivities , Phys. Rev. B 102, 165137 (2020). (open access) [被引用件数:23] (2023/4)どうでも良い話ですが、この論文は自分としてはかなり気に入っているのですが、PRLに落とされました(そのときはまだKohn公式の部分がなかったかもしれないけど)。 SPT相の論文もそうだったけど、真に革新的な論文はなかなかレフェリーに評価してもらえないのだ…
最終的にはこれはLSM定理とはほとんど別の話になったなのですが、磁化プラトーの研究・LSM定理の一般化からの一連の流れがからここに行き着いたのは確かです。 そんなわけで、ひょんなことから(?)非線形伝導の研究に取り組むことになりましたが、 現在もいろいろと関連のトピックを研究中です(2023年4月現在)。
超流動の分野で長年の謎だった「固有角運動量のパラドックス」に、平均場理論の範囲では一定の回答を与えた論文です。 詳しい内容は、「物性研だより」に解説記事 を書いたので、そちらをご覧ください。
ここには、余談的なことを書くことにします。 カイラル超流動体の角運動量を、中国からの留学生のWenxingに計算してもらいました。 まず(理想的な円盤上の)カイラルp波超伝導体の場合、BCS領域でも、全粒子がカイラルクーパー対を形成しているかのような 大きな前軌道角運動量を持つことがわかり、これをスペクトラルフローの議論で示すことができました。 これは、ある意味予想通りで、それなりに満足の行く結果でした。
そんな頃、Wenxingがカイラルd波、f波…についても計算してみる、と言い出しました(助教の多田さんがサジェストしてくれたのだったような記憶もあります)。 僕は、「そんなの、結果はp波と同じになるに決まってるんで、やってもあまり収穫がないんじゃないか」と 思ったのですが、僕がウダウダしている間に、Wenxingが計算を進めてしまいました。 すると、「d波、f波…では全角運動量がゼロになってしまう」というのです。 そんなのおかしいので、どこか計算間違ってるんじゃないか、と思ったのですが、結果的にはそれで正しかったのでした。(教訓:押川の言うことをあまり信じてはいけない!) 多田さんは、準古典理論によって、この驚くべき結果を裏付けてくれました。
それらの結果をまとめたのが上記のPRL論文ですが、arXivには2014年9月26日(金)に投稿しました。
arXiv上で公開されたのは同年9月29日(月)日本時間朝(UTC 0時以降)です。
驚いたのは、超伝導やトポロジカル物性の大家、Volovik氏が、我々の論文が公開された42時間以内に、
我々の論文に対するコメント論文を書き上げてarXivに投稿 (arXiv:1409.8638) したのでした。

さらに、その2日後くらいには、カナダMcMaster大学の Kallinらのグループが、かなりオーバーラップする内容の論文をarXivに投稿しました。 こちらは、独立に研究していて、我々の論文を見てあわてて投稿したという感じでした(ちゃんと我々の論文を引用してコメントしてくれています)が、 やはり我々の驚くべき結果(カイラルp波と、d波以上で全く結果が違う)と一致する内容でした。
そんなわけで、知らないうちに超伝導の専門家のグループと競争していた感じですが、先に論文を出せてよかったです。 Volovik氏については、競争というわけではなかったのでしょうが、彼が我々と同じようなアプローチを思いついていたら一瞬でできてしまっていたんでしょうね。

